ابن هیثم، ابوعلی

نویسنده (ها) : صادق سجادی - علیرضا جعفری نائینی

آخرین بروز رسانی : چهارشنبه 21 خرداد 1399 تاریخچه مقاله

اِبْنِ هِیْثَم، ابوعلی حسن (محمد؟) بن حسن (حسین؟) بن هیثم بصری، ریاضی‌دان برجسته و بزرگ‌ترین فیزیک‌دان و نورشناس مسلمان سدۀ ۴ ق / ۱۰ م که در آثار لاتینی سده‌های میانه به آونتان[۱] یا آوناتهان[۲] و بیشتر به آلهازن[۳] نامبردار است.

زندگی و آثار: به رغم شهرت عظیم ابن‌هیثم، اطلاعات مبسوطی دربارۀ دورانهای مختلف زندگی، خاصه تحصیلات و استادان او در دست نیست. آنچه در این‌باره می‌دانیم، غالباً روایاتی است که حدود ۳ قرن پس از او، قفطی (د ۶۴۶ ق / ۱۲۴۸ م) از یوسف فاسی (د ۶۲۴ ق / ۱۲۲۷ م) نقل کرده (ص ۱۶۷) و گاه با آنچه اندکی دیرتر، ابن ابی اصیبعه (د ۶۶۸ ق / ۱۲۷۰ م) با تفصیل بیشتر و با استناد به نوشتۀ خود ابن‌هیثم آورده و نیز روایات بیهقی و شهر زوری، متناقض است.

ابن‌هیثم اصلاً از بصره برخاست (قفطی، ۱۶۵؛ ابن ابی اصیبعه، ۲ / ۹۰) و با توجه به آنکه در ۴۱۷ ق / ۱۰۲۶ م و در ۶۳ سالگی رساله‌ای نوشت که ابن ابی اصیبعه آن را به خط خود او دیده بوده (۲ / ۹۱)، می‌بایست در ۳۵۴ ق زاده شده باشد. به روایت همو، ابن ‌هیثم چنانکه خود اشاره کرده، پس از مشاهدۀ اختلاف مردم در راههای وصول به حقیقت، به بررسی آراء و عقاید گوناگون برای یافتن راهی مطمئن به سوی حق پرداخته و چون طرفی بر نبسته، سرانجام به این اعتقاد گرویده که جز از طریق دانشی که عنصرش امور حسی و صورتش امور عقلی باشد ــ یعنی طبیعیات و الهیات و منطق ــ نمی‌توان به حق دست یافت (۲ / ۹۱-۹۲). چنین می‌نماید که وی از این پس، به تحصیل علوم طبیعی و فلسفی همت گماشت، اگرچه به مراتب تحصیلی خود هیچ اشاره‌ای نکرده است.

به روایت شیخ علم‌الدین قیصر بن ابی‌القاسم مهندس، ابن‌هیثم در بصره ــ که در آن سالها زیر فرمان آل بویۀ عراق بود ــ شغلی دیوانی داشت که از آن به وزارت بصره تعبیر شده است و چون پرداختن به علم را از آن کار دوست‌تر می‌دانست، سرانجام تظاهر به جنون کرد تا وی را عزل کردند و وی سپس به مصر رفت (همو، ۲ / ۹۰). به گفتۀ قفطی (ص ۱۶۶، ۱۶۷) سفر ابن‌هیثم به مصر به تشویق و وعدۀ الحاکم فاطمی فرمانروای مصر روی داد و البته بعید نیست که ابن‌هیثم اصلاً به امید اجرای طرح خود برای تنظیم آب نیل و برخورداری از کرم الحاکم آن تمهید را اندیشیده باشد. چه، به روایت همو، خلیفۀ فاطمی پس از اطلاع از این طرح، مالی برای ابن‌هیثم فرستاد و او را به سفر به مصر تشویق کرد. چون ابن‌هیثم به آن دیار رسید، خلیفه خود به استقبال او بیرون شد و دانشمند را گرامی داشت. ابن‌هیثم اندکی بعد در رأس گروهی از مهندسان به بررسی نیل و مجرای آن در بخش مرتفع جنوب مصر پرداخت، اما با مشاهدۀ آثار و ابنیه‌ای که مصریان براساس طرحهای دقیق هندسی ساخته بودند، دریافت که اگر اجرای طرحی که او در اندیشه داشت، ممکن بود، این مصریان فرهیختۀ دانا به هندسه و ریاضیات، البته پیش‌تر به آن دست می‌زدند.

بررسی چگونگی مرتفعات اسوان که نیل از آن می‌گذرد، نیز این نتیجه‌گیری را تأیید کرد. ازاین‌رو نزد خلیفه به ناکامی خود اعتراف کرد. ظاهراً خلیفه واکنش تندی از خود نشان نداد، اما چنین می‌نماید که از این ناکامی چندان خشمناک شده بود که ابن‌هیثم را به جای آنکه در جایی چون دارالحکمۀ قاهره، در کنار کسانی مانند ابن‌یونس منجم به کار بگمارد، به شغلی دیوانی گماشت. ابن‌هیثم با آنکه از بیم این فرمانروای خونریز، به این شغل گردن نهاد، ولی برای رهایی از آن چاره در این دید که باز تظاهر به جنون کند. ازاین‌رو خلیفه اموال او را مصادره کرد و کسی را به قیمومتش گماشت و در خانه‌اش محبوس کرد. چون الحاکم درگذشت (۴۱۱ ق / ۱۰۲۰ م)، ابن‌هیثم نیز از تظاهر به جنون دست برداشت و آزاد شد و اموالش را باز پس گرفت. وی نزدیک الازهر قاهره مقام گزید و بقیۀ عمر را به تدریس و تألیف سپری کرد و از طریق استنساخ کتاب روزی خود را به دست می‌آورد (ابن ابی اصیبعه، ۲ / ۹۱).

بیهقی بر آن است که ابن‌هیثم رساله‌ای دربارۀ تنظیم آب نیل نوشت و به مصر رفت، اما الحاکم از همان آغاز ورود او، پس از بررسی طرح مذکور، آن را کم فایده و پرهزینه خواند و با ابن‌هیثم درشتی کرد. ابن‌هیثم از بیم خلیفه شبانه به شام گریخت و به خدمت یکی از امرای آن دیار درآمد به رغم بخششهای این امیر به مختصری قناعت کرد و یکسره به کارهای علمی پرداخت (ص ۷۸)، اما شهرزوری (۲ / ۳۰) پس از تکرار سخن بیهقی، به نقل روایت دیگری می‌پردازد که بر پایۀ آن، ابن‌هیثم نخست در شام می‌زیسته و از آنجا به مصر رفته است. از سوی دیگر به نظر نمی‌رسد که ابن‌هیثم همۀ عمر را پس از مرگ الحاکم در قاهره مانده باشد. چه، از پاسخی که به یک سؤال هندسی در ۴۱۸ ق در بغداد داده (ابن ابی اصیبعه، ۲ / ۹۷)، معلوم می‌شود که لااقل در آن سال در بغداد بوده، ولی دوباره به مصر بازگشته، زیرا قاضی ابوزید عبدالرحمن بن عیسی او را در ۴۳۰ ق / ۱۰۳۹ م در آن دیار دیده بوده است (صاعد اندلسی، ۶۰).

از تاریخ درگذشت ابن‌هیثم اطلاعی در دست نیست. غالب نویسندگان مرگ او را در حدود سال ۴۳۰ ق یا پس از آن در قاهره دانسته‌اند (مثلاً: ابن‌عبری، ۱۸۳). قفطی (ص ۱۶۷) یادآوری کرده که رساله‌ای به خط او دیده شده که تاریخ ۴۳۲ ق بر آن کتابت شده بوده است. به گفتۀ بیهقی (ص ۸۰) چون به سختی بیمار شد و دانست که عمرش به سر آمده، خود روی به کعبه خوابید و ذکر حق گفت و درگذشت.

ابن‌هیثم به روزگاری برآمد که اوج شکوفایی علوم در تمدن اسلامی به شمار است. وی از میراث علمی عظیمی که از تمدنهای کهن‌تر به جهان اسلام راه یافته و به دست دانشمندان برجسته‌ای شرح و بسط داده شده بود، بهره‌ها برد.

ابن‌هیثم را باید پیشرو دانشمندان اهل تجربه و آزمایش به معنای دقیق آن خواند. زیرا وی در نظریات علمی خود، به‌ویژه در بررسیهای نورشناسی و مسألۀ اِبصار، به درستی از استقراء و تمثیل و قیاس سود می‌جست. چنانکه گفته‌اند، در به کارگیری روش استقراء علمی، گذشته از تقدم زمانی بر فرانسیس بیکن، دیدگاهی وسیع‌تر و عمیق‌تر از او نیز داشته است (نظیف‌بک، ۱ / ۳۱-۳۳). وی علاوه بر ریاضیات و نورشناسی، در فنونی چون کلام، مابعدالطبیعة، منطق، اخلاق، ادب و موسیقی ماهر بود و خاصه در قوانین نظری و امور کلی پزشکی دستی قوی داشت، ولی به طبابت نپرداخت (ابن ابی اصیبعه، ۲ / ۹۰، ۹۲، ۹۳). بیهقی او را بطلمیوس ثانی لقب داده و از زهد دینداری او یاد کرده است (ص ۷۷، ۷۹؛ نیز نک‌ : ابن ابی اصیبعه، ۲ / ۹۰).

از میان شاگردان ابن‌هیثم، در طول سالهایی که به تدریس اشتغال |داشت، فقط دو تن را می‌شناسیم: ابوالوفاء مبشر بن فاتک، دانشمند مشهور مصری که نزد ابن‌هیثم به تحصیل ریاضی پرداخت (همو، ۲ / ۹۸- ۹۹) و یکی از بزرگان سمنان به نام سرخاب (سهراب) که ۳ سال نزد او شاگردی کرد و استاد هر ماه ۱۰۰ دینار از او می‌گرفت، اما چون درس به انجام رسید، ابن هیثم همۀ آنچه را که گرفته بود، به سرخاب باز پس داد و یادآور شد که مراد او از این کار، آزمایش خلوص شاگرد در دانش‌اندوزی بوده است (بیهقی، ۷۸- ۷۹).

ابن‌هیثم به زبان عربی مسلط بود و خطی خوش داشت (ابن ابی اصیبعه، ۲ / ۹۰). کتابهایی که وی استنساخ می‌کرد، گذشته از خط خوش، از دقت علمی بسیار نیز برخوردار بود و طالبان این کتابها مبالغ زیادی در ازای آن می‌پرداختند (قفطی، همانجا).

آثـار

اگرچه ابن‌هیثم از دانشمندان کثیرالتألیف به شمار است، ولی حجم بسیاری از آثار او در فنون مختلف از چند برگ تجاوز نمی‌کند. او در نخستین مرحلۀ تألیف، آثار متقدمان را شرح یا تلخیص می‌کرد. گاه نیز به رد آراء یکی و دفاع از دیگری می‌پرداخت، مانند رسالة فی بطلان مایراه المتکلمون من أن اللـه لم یزل غیرفاعل ثم فعل و الرد علی یحیی النحوی مانقضه علی ارسطو طالیس و غیره من اقوالهم فی السماء و العالم. برخی دیگر از آثار او مانند استخراج سمت القبله و استخراج مابین بلدین فی البعد بجهة الامور الهندسیة منطبق با نیازهای علمی جامعه است، اما مهم‌ترین و برجسته‌ترین آثار خود مانند المناظر را در سومین دورۀ زندگی پس از مرگ الحاکم فاطمی و اشتغال مجدد به تدریس و تصنیف نوشته است (ابن ابی اصیبعه، ۲ / ۹۴-۹۵؛ نظیف بک، ۱ / ۱۳-۱۵).

ابن‌هیثم در رسالۀ علوم الاوائل، آثار خود را تا ۴۱۷ ق، ۷۰ رساله بر شمرده (۲۵ اثر در ریاضیات، ۴۴ اثر در طبیعیات و الهیات و یک اثر در علوم اوائل) و گویا اینها بجز رسائلی بوده که مردم اهواز و بصره از او در دست داشتند (ابن ابی اصیبعه، ۲ / ۹۳-۹۶). در جمادی‌الآخر ۴۱۹ او خود در دنبال آثار پیشین در همان کتاب، نام ۲۱ اثر دیگر او را تا آخر ۴۲۹ ق / ۱۰۳۸ م گرد آورده و همۀ این ۹۲ اثر را تقریباً به ترتیب زمانی مرتب کرده است (صبره، ۱۹۰). بعضی از مقالات و رسایل ابن‌هیثم از یک سده پیش به این طرف توسط محققان مسلمان و اروپایی تجزیه و تحلیل و ترجمه و منتشر شده است. چند اثر از مهم‌ترین آثار او از این قرار است:

۱. آلة لفحص الضوء و انکساره. این رساله را ویدمان از متن لاتینی به آلمانی ترجمه و در ۱۸۸۴ م در «اخبار فیزیک[۴]» منتشر کرده است. سزگین مجدداً همین مقاله را در جلد اول مجموعه مقالاته ویدمان به چاپ رسانیده است.

۲. استخراج ارتفاع القطب علی غایة التحقیق. نسخه‌های متعددی از آن در کتابخانه‌ها موجود است (GAS, V / 366, VII / 411؛ بخیت، ۳ / ۱۲۹؛ ورهووه، 188). کارل شوی[۵] آن را بررسی کرده و نتیجۀ این بررسی را در جلد اول مجموعه مقالات خود به چاپ رسانده است.

۳. استخراج اعمدة الجبال، که نسخه‌ای از آن ضمن مجموعه‌ای در بادلیان نگهداری می‌شود (بخیت، ۳ / ۱۲۸- ۱۲۹).

۴. استخراج سمت القبلة فی جمیع المسکونة بجداول و صفتها و لم اورد البرهان علی ذلک. نسخی از آن در لنینگراد و بادلیان موجود است (همو، ۳ / ۱۲۹؛ خالدوف، I / 457). این مقاله را کارل شوی بررسی و در ۱۹۲۱ م در «مجلۀ انجمن خاورشناسی آلمان[۶]» منتشر کرده است. سزگین نیز بعداً همین مقاله را در جلد اول مجموعه آثار شوی منتشر کرد.

۵. مقالة مختصرة فی الاشکال الهلالیة و مقالة مستثصاة فی الاشکال الهلالیة، که نسخه‌های متعددی از این دو رساله در لنینگراد و و ادارۀ هند لندن، برلین شرقی و مونیخ نگهداری می‌شود (خالدوف، GAL, I / 618; GAS, V / 365-366, VII / 411; I / 453).

۶. اضواء الکواکب. نسخه‌هایی از این اثر در کتابخانه‌ها موجود است ( آلوارت، GAS, VI / 259; V / 155). این رساله را ویدمان در ۱۸۹۰ م بررسی و به اختصار به آلمانی ترجمه و در «هفته‌نامۀ ستاره‌شناسی...[۷]» منتشر کرده است. سزگین بعداً همان را در جلد اول مجموعه مقالات ویدمان چاپ کرده است. در ۱۹۵۷ م نیز در حیدرآباد دکن به چاپ رسیده است.

۷. برکار الدوائر العظام یا استعمال برجل (برکار) لرسم الدوائر العظام، که نسخه‌های متعددی از آن موجود (خالدوف، GAS, V / 370; I / 452). این مقاله را ویدمان بررسی و در ۱۹۱۰ م در «مجلۀ مساحی[۸]» منتشر کرده است. سزگین همین مقاله را بعداً در جلد اول مجموعه مقالات ویدمان چاپ کرده است.

۸. تربیع الدائرة، که زوتر[۹] آن را همراه با ترجمۀ آلمانی در ۱۸۹۹ م در «مجلۀ ریاضیات و فیزیک[۱۰]» منتشر کرد. سزگین بعداً همین رساله را در ۱۹۸۶ م در جلد دوم مجموعه مقالات زوتر چاپ کرد.

۹. حرکة القمر. نسخه‌هایی از این اثر در استانبول، بادلیان و لنینگراد موجود است ( خالدوف، GAS, VI / 257; I / 457).

۱۰. حل شکوک حرکة الالتفاف. ابن‌هیثم این رساله را در جواب ایرادهایی نوشت که به رسالۀ او موسوم به حرکة الالتفاف وارد کردند (از خود رسالۀ مذکور هیچ نشانی در دست نیست). عبدالحمید صبره این رساله را با خلاصه‌ای به زبان انگلیسی در مجلۀ تاریخ العلوم العربیة (حلب، ۱۹۷۹ م، ج ۳، شم‌ ‌۲) چاپ کرده است.

۱۱. رسالة فی صورة الکسوف، که نسخه‌هایی از آن در بادلیان، لندن، استانبول و لنینگراد موجود است (خالدوف، همانجا؛ GAS , VI / 252؛ بخیت، همانجا). مقدمۀ این رساله را ویدمان به آلمانی ترجمه کرده و روشن ساخته است که نخستین کاربرد تاریکخانه در تاریخ نورشناسی از سوی ابن‌هیثم صورت گرفته است. این مقاله در ۱۹۱۰ م در «سالنامۀ عکاسی[۱۱]» منتشر شد. سزگین نیز بعداً آن را در جلد اول مجموعه مقالات ویدمان چاپ کرد.

۱۲. رسالة فی مساحة المجسم المکافی، که یکی از مهم‌ترین آثار ریاضی اسلامی است (نک‌ : بخش تجزیه و تحلیل برخی از آثار ابن‌هیثم در همین مقاله).

۱۳. الضوء، که نخستین‌بار توسط بارمن[۱۲] ترجمه و در ۱۸۸۲ م در «مجلۀ انجمن خاورشناسی آلمان»، چاپ شد. ویدمان نیز تحریر همین رساله را که توسط کمال‌الدین فارسی (د ۷۲۰ ق / ۱۳۲۰ م) انجام شده است، بررسی و در همان مجله منتشر کرد. بعداً سزگین همان را در جلد اول مجموعه مقالات ویدمان چاپ کرد. این رسالۀ ابن‌هیثم همچنین در ۱۹۶۹ م در مقالات ابن‌هیثم، به مناسبت جشن هزارۀ او، به کوشش احمداللـه ندوی در پاکستان منتشر شد. در ۱۹۸۳ م نیز در حیدرآباد دکن همراه مجموع الرسائل ابن‌هیثم چاپ شد.

۱۴. ضوء القمر، ابن‌رضوان پزشک مشهور مصری در ۴۲۲ ق آن را برای خود استنساخ کرد و از اینجا پیداست که در ایام خود مؤلف این اثر شهرتی یافته بوده است (قفطی، ۴۴۴). این رساله نیز در مقالات ابن‌هیثم به کوشش نعیم‌الدین زبیری منتشر شد.

۱۵. المرایا المحرقة بالدوائر، که توسط وینتر[۱۳] و عرفات به انگلیسی ترجمه و تجزیه و تحلیل و در ۱۹۵۰ م در «مجلۀ انجمن سلطنتی آسیایی بنگال[۱۴]» چاپ شده است. در ۱۹۸۳ م نیز در مجموع الرسائل در حیدرآباد دکن به چاپ رسید.

۱۶. المرایا المحرقة بالقطوع، که توسط وینتر و عرفات به انگلیسی ترجمه شد و ضمن نشر در «مجلۀ انجمن سلطنتی آسیایی بنگال» مورد تجزیه و تحلیل قرار گرفت. در ۱۹۶۹ م نیز در مقالات ابن‌هیثم به کوشش علی ناصر زیدی در پاکستان چاپ شد و در ۱۹۸۳ م در حیدرآباد دکن نیز در مجموع الرسائل ابن‌هیثم منتشر گردید.

ویدمان هر دو رسالۀ پیش را بررسی و با نام «تاریخ آیینه‌های سوزان[۱۵]» در ۱۸۹۰ م در «اخبار فیزیک» منتشر کرده است. سزگین بعداً همین بررسی را در جلد اول مجموعه مقالات ویدمان چاپ کرد.

۱۷. المناظر، معروف‌ترین کتاب ابن‌هیثم شامل ۷ مقاله است. نسخه‌های متعددی از آن در کتابخانه‌ها موجود است. ترجمۀ لاتینی این کتاب در قرون وسطی، تأثیر عمیقی در دانش غربی نهاد و پیشرفت عظیمی را در روش تجربی به بار آورد (سارتن، ۱ / ۸۲۷). این کتاب توسط کمال‌الدین فارسی با عنوان تنقیح المناظر لذوی الابصار و البصائر نقد و تهذیب شده در حیدرآباد (۱۳۴۷- ۱۳۴۸ ق) در ۲ مجلد به چاپ رسیده است. ویدمان چند فصل اول کتاب تنقیح المناظر را به آلمانی ترجمه و با عنوان «نورشناسی ابن‌هیثم»[۱۶] در ۱۹۱۲ م در مجلۀ «آرشیو تاریخ علوم طبیعی ... [۱۷]» منتشر کرد. این مقاله بعداً توسط سزگین در جلد اول مجموعه مقالات ویدمان چاپ شده است. همچنین ویدمان بخشی دیگر از تنقیح المناظر کمال‌الدین را ترجمه کرده که در جلد اول مجموعه مقالات وی چاپ شده است.

۱۸. الشکوک علی بطلمیوس. در این اثر ابن‌هیثم ۳ کتاب بطلمیوس یعنی المجسطی، الاقتصاص و المناظر را مورد ارزیابی و نقد قرار داده است. وی به رغم اعتراف به مقام علمی «مردی که به فضلیت مشهور و در ریاضیات متبحر است»، تصریح می‌کند که «در کتابهای وی مواضع شبهه‌ناک و الفاظ نادرست و معانی متناقض یافته است، گرچه این موارد در قیاس با معانی درست کتابهای وی اندک است» (ابن‌هیثم، ۴). این اثر در ۱۹۷۱ م به کوشش عبدالحمید صبره و نبیل شهابی در قاهره به چاپ رسیده است.

۱۹. مقالة فی هیئة العالم. ابن‌هیثم خود این اثر را در شمار مؤلفات طبیعی ـ الهی خویش نهاده است (ابن‌اصیبعه، ۲ / ۹۴). دو ترجمۀ عبری از این مقاله در دست است و ۳ ترجمۀ لاتین آن نیز شناخته شده است که یکی از آنها از یک ترجمۀ اسپانیایی که اکنون در دست نیست، برگردانده شده است. در سدۀ ۶ ق نیز محمد بن احمد خَرَقی شرحی به زبان عربی بر آن نوشت. در نیمۀ دوم سدۀ ۸ ق / ۱۴ م میرسید شریف جرجانی آن را به فارسی ترجمه و شرح کرد. بخشی از آن (دربارۀ زمین) در ۱۹۰۹ م از سوی ویدمان به آلمانی ترجمه شد. کول نیز بخش دیگری از آن را دربارۀ اجرام آسمانی و حرکات آنها در ۱۹۲۲ م به همین زبان برگرداند (شرام، 6, 15, 63-64؛ زرکلی، ۵ / ۳۱۷؛ لوت، 734).

به گفتۀ شتاین شنایدر، ابن‌هیثم رساله‌ای نیز در فضیلت مطلق دانش داشته و آنچه ابن ابی اصیبعه دربارۀ او و تألیفاتش آورده، از همین رساله نقل شده است (نک‌ : شرام، 9)، اما شواهد صحت این استنباط را نفی می‌کند.

مآخذ

در پایان مقاله.

سیدصادق سجادی

جایگاه ابن هیثم در تاریخ علم

خاورشناسان اروپایی به پژوهشهای گسترده‌ای دربارۀ آثار ابن‌هیثم پرداخته و با ابراز شگفتی بسیار تواناییهای این دانشمند نوآور را تحسین کرده و مقام او را در تاریخ علم بسیار والا شمرده‌اند. تا پایان سدۀ ۱۹ م وی بیشتر به دلیل آثارش در نورشناسی مورد ستایش قرار می‌گرفت، اما وقتی کسانی چون ویدمان، زوتر، شوی، شرام و نیز مصطفی نظیف بک به بررسی و معرفی مفصل‌تر آثار او پرداختند، آشکار شد که ابتکار حل شماری از مسائل دشوار ریاضیات نیز از آن اوست.

کارل شوی در مقدمۀ ترجمۀ رسالۀ استخراج سمت القبلة دربارۀ وی گوید: نوشته‌های ابن‌هیثم نشان می‌دهد که این دانشمند، با تبحر بسیار توانسته است مسائل دشوار مثلثات را نیز از راههای صرفاً هندسی حل کند (ص 243-244؛ نیز نک‌ : GAS, V / 362). سارتن وی را بزرگ‌ترین نمایندۀ روح تجربی در سده‌های میانه خوانده است (۱ / ۷۹۷). ماتیاس شرام استعداد نبوغ‌آمیز ابن‌هیثم را در ریاضیات می‌ستاید و در شرح ابن‌هیثم بر مجسطی و نیز حل الشکوک فی کتاب المجسطی، بر مطالبی که برای ارزیابی ابن‌هیثم به عنوان ریاضی‌دان مناسب یافته، تأکید ورزیده است. همو، پژوهشهای ابن‌هیثم در نورشناسی را نیز گواه بر استعداد فوق‌العادۀ وی در ریاضیات می‌شمارد. به گفتۀ وی گرچه ابن‌هیثم، همانگونه که در شرح سلوک علمی خویش آورده، نخست پیرو ارسطو بوده است، اما پژوهشهای وی در علوم دقیقه و تعمق او در فلسفه و ریاضیات موجب شد که از آن عقیدۀ نخستین برگردد و بدین‌سان، شیوۀ علمی ابن‌هیثم، از اعتبار احکام جزمی ارسطو کاست.

ابن‌هیثم مبتکر روشهای تجربی است و آزمایش علمی به عنوان یکی از وسایل سیستماتیک کار، دستاورد ابن‌هیثم است. تحول جهش‌وار دانش نورشناسی در آثار مربوط به مکتب اکسفورد، تا حدود زیادی مرهون آشنایی با منابع عربی و به‌ویژه آثار ابن‌هیثم بوده است. شرام با بررسی تفصیلی ۳ اثر از ابن‌هیثم، یعنی ضوء القمر، المناظر و هیئة العالم، بر آن است که ابن‌هیثم کوشیده است میان طبیعیات ارسطویی از یک سو و ریاضیات به کار رفته در ستاره‌شناسی و نورشناسی کهن، پیوندی برقرار سازد و این تلاش، به‌ویژه در ۳ کتاب یاد شده، نمونه‌وار است (شرام، 3-8, 14؛ نیز نک‌ : GAS, V / 364).

راجر بیکن، دانشمند انگلیسی سدۀ ۱۳ م در تحقیقات علمی خویش از نتایج پژوهشها و آزمایشهای ابن‌هیثم استفادۀ فراوان برده است، کاربرد ریاضیات در پژوهشهای مربوط به علوم طبیعی، از جمله شیوه‌هایی است که راجربیکن را پایه‌گذار آن می‌شناسند، درحالی‌که استفاده از ریاضیات در دانشهای طبیعی از سوی ابن‌هیثم به‌ویژه در المناظر و المرایا المحرقة به روشن‌ترین وجه و بسیار جدی‌تر از آنچه بیکن انجام داده، صورت گرفته است (ویدمان، II / 771).

خاورشناسان دقت ابن‌هیثم را در مقالۀ الشکوک علی بطلمیوس ستوده‌اند. در این اثر، وی تفاوتها و تناقضات میان دو اثر نجومی بطلمیوس، یعنی المجسطی و الاقتصاص را آشکار می‌سازد و نظریات دقیق‌تری را عرضه می‌دارد. همچنین در فی هیئة العالم می‌کوشد آنچه را بطلمیوس در الاقتصاص ناتمام گذارده، تکمیل کند (صبره، «س ـ ص»؛ GAS, V / 362). تحول دانش ستاره‌شناسی در مغرب زمین، بیش از همه مدیون این کتاب است. هارتنر ثابت کرده است که نظریۀ سیارات نو که در سدۀ ۱۵ م از جانب پورباخ بیان شده، در اساس چیزی جز تکرار نظریۀ ابن‌هیثم نبوده است. نظریۀ سیارات نو، به نوبۀ خود بزرگ‌ترین تأثیر را بر روی کپرنیک، رکیومونتان و راینهولد باقی گذارد (شرام، GAS, VI / 251; 63-64).

پژوهشهای ابن‌هیثم دربارۀ نور ماه، از نظر کول که رسالۀ ضوء القمر را به آلمانی ترجمه کرده، نخستین تلاش در جهت یک تحقیق جامع فیزیک نجومی به شمار می‌آید و این واقعیت که ابن‌هیثم در این اثر، با ابزارهای آزمایش به پژوهش در اشعۀ ماه پرداخته و نخستین‌بار از «تاریکخانه» استفاده کرده، جایگاه او را به عنوان پژوهشگر طبیعی، بلکه پایه‌گذار روش نوین پژوهش طبیعت، نشان می‌دهد (GAS, VI / 253).

مآخذ

در پایان مقاله.

بخش علوم

تجزیه و تحلیل برخی از آثار ابن‌هیثم

رسالة فی مساحة المجسّم المکافی، یکی از مهم‌ترین آثار ریاضی اسلامی است. در این رساله ابن‌هیثم روش افناء را برای پیدا کردن حجمهایی که برخی از آنها (مسائل ۴، ۵ و ۶ در این مقاله) تا زمان خود او محاسبه نشده بودند، به کار برده است. به این ترتیب ابن‌هیثم قادر شد که در محاسبۀ حجم حاصل از دوران، محور دوران را برای اولین‌بار به‌طور دلخواه انتخاب کند. قبل از ابن‌هیثم، ارشمیدس مسائل ۱، ۲ و ۳ را که ذیلاً دربارۀ آنها صحبت می‌شود، با روش افناء (گرچه کمی متفاوت با روش ابن‌هیثم) حل کرده بود.

قابل ذکر است که به احتمال زیاد دانشمندان اسلامی از جمله ابن‌هیثم از نسخه‌ای که ارشمیدس دربارۀ روش افناء نوشته بود، نسخۀ مربوط به شبه‌مخروطها و شبکه‌کره‌ها، اطلاعی نداشتند، چون در هیچ‌یک از منابع اسلامی ذکری از آن نشده است.

تکامل روش افناء درواقع منجر به نظریۀ انتگرال گردید که پایۀ مهم کاربرد ریاضیات در مسائل عملی و نظری است.

ابن‌هیثم راجع به تحقیقات ثابت ابن‌قره و ابوسهل کوهی در این رساله صحبت کرده است. وی به صراحت گفته است که آن دو فقط راجع به مسائل ۱، ۲ و ۳ بحث کرده‌اند.

این رساله بین سالهای ۱۹۱۱-۱۹۱۲ م توسط هاینریش زوتر به آلمانی ترجمه و تجزیه و تحلیل شده است (GAS, V / 365). در تجزیه و تحلیلی که اینک انجام می‌گیرد، سعی شده است تا نقایص کار زوتر که بیشتر در اشکال و مقایسۀ کارهای ابن‌هیثم با فرم محاسباتی امروزی مشهود است، برطرف گردد. در اینجا راه حل ابن‌هیثم برای مسائل ۱ و ۴ به تفصیل، با نمادهای جدید بیان می‌شود.

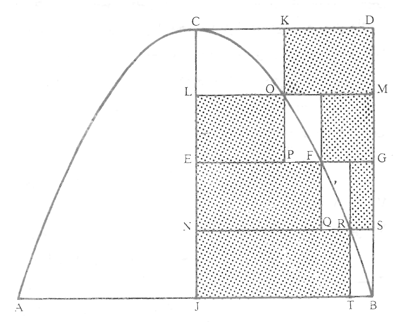
مسألۀ ۱

سهمی ACB مانند شکل ۱ مفروض است. محور تقارن سهمی CJ است. سهمی را حول CJ دوران می‌دهیم. می‌خواهیم حجم حاصل از دوران یعنی V را حساب کنیم. ابن‌هیثم ثابت می‌کند که

و W حجم استوانۀ حاصل از دوران مستطیل CB حول CJ است.

اثبات ابن‌هیثم به این صورت است:

شکل ۱

مرحلۀ اول ـ پاره‌خط CJ را به دو قسمت مساوی تقسیم می‌کنیم و نقطۀ وسط را E می‌نامیم. از E خطی موازی AB رسم می‌کنیم تا قوس CB از سهمی را در نقطۀ F و خط DB را در نقطۀ G قطع کند. از F خطی مانند IH به موازات CJ رسم می‌کنیم، قسمت هاشور خوردۀ داخل سهمی را حول CJ دوران می‌دهیم، حجی که متناظر با قسمت هاشور نخوردۀ داخل سهمی بر اثر دوران حول CJ تولید می‌شود، حجم باقی‌ماندۀ داخلی می‌نامیم. عبارت «حجم باقی‌ماندۀ خارجی» نیز معنی مشابهی دارد.

در این مرحله داریم:

= حجم باقی‌ماندۀ داخلی حاصل از دوران V-

(1)

= حجم باقی‌ماندۀ خارجی حاصل از دوران V+

(2)

مرحلۀ دوم ـ حال فاصلۀ EJ را به دو قسمت مساوی و فاصلۀ CE را نیز به دو قسمت مساوی تقسیم می‌کنیم مانند شکل ۲. L وسط CE و N وسط JE قرار دارد. مجدداً از نقاط N، E، L خطوطی به موازات AB رسم می‌کنیم تا قوس CB از سهمی را به ترتیب در نقاط R، F، O و خط BD را در S، G، M قطع کنند. از شکل ۲ داریم:

= حجم باقی‌ماندۀ داخلی V-

(۳)

= حجم باقی ماندۀ خارجی V+

(۴)

باتوجه به اینکه ACB یک سهمی است، عددی مثبت مانند μ موجود است، به‌طوری که فرمولهای (1) و (2) در مرحلۀ اول به ترتیب به صورتهای ( ) و ( ) در می‌آیند:

( ) = حجم باقی‌ماندۀ داخلی V-

شکل ۲

= حجم باقی‌ماندۀ خارجی V+

( )

و فرمولهای (۳) و (۴) در مرحلۀ دوم به ترتیب به صورتهای (۳) و ( ) در می‌آیند:

= حجم باقی‌ماندۀ داخلی V-

( )

= حجم باقی‌ماندۀ داخلی V+

( )

پس در مرحلۀ nام پس از اینکه CJ را به ۲n قسمت مساوی تقسیم می‌کنیم، خواهیم داشت:

= حجم باقی‌ماندۀ داخلی V-

( )

= حجم باقی‌ماندۀ خارجی V+

( )

اکنون می‌گوییم: V باید مساوی باشد، زیرا اگر چنین نباشد، تنها دو حالت دیگر امکان دارد:

حالت اول:

v> w

در این حالت فرض می‌کنیم که

S = V - W

پس S مثبت است، حال در مرحلۀ nام واضح است که

= حجم باقی‌ماندۀ خارجی + حجم باقی‌ماندۀ داخلی (مثلاً در مرحلۀ اول در شکل ۱، حجم حاصل از دوران قسمتهای هاشور نخوردۀ طول CJ مساوی است با حجم حاصل از دوران مستطیل DE حول محور CJ، و درنتیجه مساوی است. به همین ترتیب در مرحلۀ دوم شکل ۲ حجم حاصل از دوران مستطیلهای هاشور نخوردۀ حول محور CJ، مساوی با حجم حاصل از دوران مستطیل CM حول محور CJ است و درنتیجه برابر است با ).

پس از مرحله‌ای مانند m به بعد، با ریزتر کردن تقسیمات CJ، داریم:

(۵) (۶) اکنون از (۵) باتوجه به اینکه

V - W = S

داریم: (۷) w > حجم باقی‌ماندۀ داخلی V-

از (۷) و ( ) برای n>m داریم:

از (۸)با در نظر گرفتن اینکه

W=π(JB)۲ (CJ)-μ π(CJ)۲

داریم:

(۹)

اکنون ابن‌هیثم با استفاده از فرمول

(k صحیح و مثبت است) که قبلاً به عنوان یک قضیۀ کمکی ثابت کرده است، از (۹)، نامساوی زیر را به دست می‌آورد:

یعنی:

که محال است. این تناقض نشان می‌دهد که حالت اول ممکن نیست.

حالت دوم: V< W

در این حالت مجدداً قرار می‌دهیم: S = W-V

و از یک مرحله مانند m به بعد (۶) برقرار است، اکنون می‌نویسیم:

< S حجم باقی‌ماندۀ خارجی

W-V=S

درنتیجه: (۱۰) V< W + حجم باقی‌ماندۀ خارجی از (۱۰) و ( ) برای n>m داریم:

و از اینجا داریم:

و در نتیجه:

بنابراین:

این تناقض نشان می‌دهد که حالت دوم نیز ممکن نیست، پس

V= W

و قضیه ثابت است.

البته با روش انتگرال‌گیری مدرن محاسبۀ W به صورت زیر است:

در شکل ۳ معادلۀ سهمی را طبق معمول به صورت

Y = α (r۲-x۲)

می‌گیریم و داریم:

شکل ۳

(حجم حاصل از دوران مستطیل OD حول محور yها).

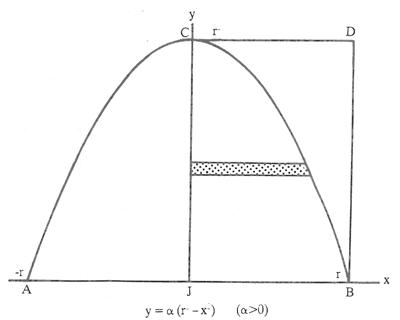
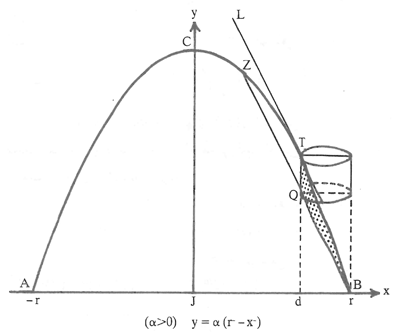
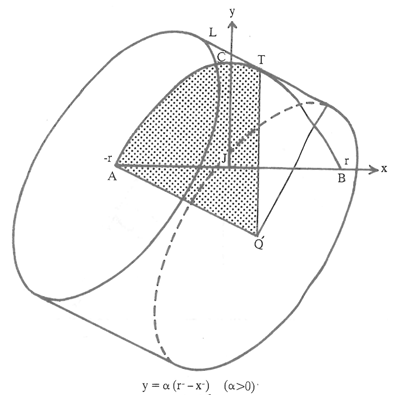
مسألۀ ۲

حجم حاصل از دوران قسمت هاشور خورده در شکل ۴ حول محور dT مساوی است با حجم استوانۀ قائم مستدیری که ارتفاع آن QT است و شعاع قاعدۀ آن dB است.

T نقطه‌ای است روی قوس CB از سهمی که در آن نقطه، مماس بر سهمی (خط L) با قاطع BZ موازی است و Q محل تقاطع عمود از نقطۀ T بر خط AB با قطعۀ ZB است.

شکل ۴

اثبات ابن‌هیثم را برای مسألۀ ۲ بیان نمی‌کنیم، ولی مناسب است که اثبات امروزی آن را بنویسیم که معلوم شود با فقدان شیوه‌های جدید ابن‌هیثم چه کار مهمی انجام داده است.

ضریب زاویۀ خط L عبارت است از -۲αd درنتیجه معادلۀ خط قاطع BZ عبارت است از: y=-۲αd(x-r)

درنتیجه عرض نقطۀ Q عبارت است از:

-۲αd(d-r)=۲αd(r-d) (۱۱)

اکنون با طریقۀ پوسته‌های استوانه‌ای حجم حاصل از دوران قسمت هاشور خوردۀ حول محور Qd عبارت است از:

(۱۲(

از طرفی مطابق (۱۱) داریم:

= -۲αd(r-d) عرض نقطۀ T = ارتفاع استوانه = QT

α(r۲-d۲)-۲αd(r-d)=a(r-d)۲

درنتیجه حجم استوانۀ مورد بحث برابر است با

α(r-d)۲ π(r-d)۲=πα(r-d)۴

از اینجا و (۱۲) مسأله ثابت می‌شود.

مسألۀ ۳

حجم حاصل از دوران قسمت هاشور خورده در شکل ۵، حول محور dT مساوی است با حجم استوانۀ قائم مستدیری که ارتفاع آن QT و شعاع قاعدۀ آن dA است (T نقطه‌ای است روی قوس CB از سهمی که در آن نقطه مماس بر سهمی (خط L) با قاطع AQ موازی است و Q محل تقاطع عمود از نقطۀ T بر خط AB با قاطع مزبور است).

مجدداً یادآور می‌شویم که مشابه راه حل امروزین مسألۀ ۲، به آسانی می‌توان نشان داد که QT=α(r+d)۲

درنتیجه حجم استوانۀ مورد بحث عبارت است از: πα(r+d)۴

و در این مورد

شکل ۵

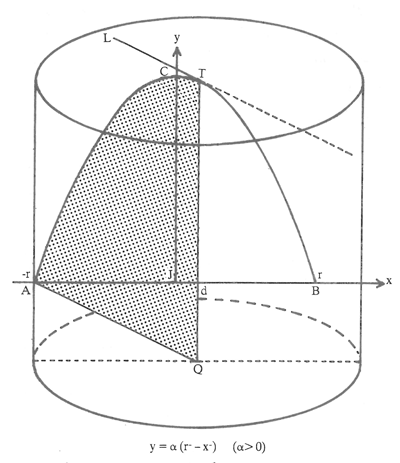
مسألۀ ۴

سهمی ACB مانند شکل ۶ مفروض است، محور تقارن سهمی CJ است. قوس CB را حول JB دوران می‌دهیم، می‌خواهیم حجم حاصل از دوران یعنی V را حساب کنیم.

ابن‌هیثم ثابت می‌کند که V= W

که در آن W حجم استوانۀ حاصل از دوران مستطیل CB حول JB است.

اثبات ابن‌هیثم به این صورت است که JB را به ۲n قسمت مساوی تقسیم می‌کند.

(در شکل ۶، n=۲ و JK = KL = LM = MB)

واضح است که رابطۀ زیر برقرار است:

+ حجم قسمت باقی‌ماندۀ داخلی در اثر دوران حول JB

(۱۳) = حجم قسمت باقی‌ماندۀ خارجی در اثر دوران حول JB

برای اثبات مسألۀ فوق، ابن‌هیثم قبلاً نامساویهای زیر را ثابت می‌کند:

(n۲-۱۲)۲+(n۲-۲۲)۲+…+(n۲-(n-۱)۲)۲< n۵ (۱۴)

(۲۲)۲+(n۲-۱۲)۲+(n۲-۲۲)۲+…+(n۲-(n-۱)۲)۲> n۵ (۱۵)

برای اثبات این نامساویها ابن‌هیثم فرمولهای زیر را ثابت می‌کند:

۱+۲+…+n=

۱۲+۲۲+…+n۲=

۱۴+۲۴+…+n۴=

لازم به تذکر است که برای اثبات هر یک از ۴ فرمول فوق به فرمولهای ماقبل آن در (۱۶) نیاز است و ۳ فرمول نخستین قبل از ابن‌هیثم شناخته شده بود، ابن‌هیثم چهارمین فرمول را به منظور کمک به اثبات نامساویهای (۱۴) و (۱۵) برای اولین بار به‌طور دقیق ثابت می‌کند. اثبات ابن‌هیثم بیشتر جنبۀ هندسی دارد و درواقع جای‌گزینی از فرمولهای (۱۶) در طرف چپ نامساویهای (۱۴) و (۱۵) پس از بسط دادن آنهاست.

شکل ۶

در شکل ۶ داریم: = حجم باقی‌ماندۀ داخلی V-

= حجم حاصل از دوران قسمت هاشور خورده حول محور JB

(۱۷)

و چون CB یک قوس از سهمی است، می‌توان نوشت:

(۱۸)

و با توجه به اینکه

از (۱۷) می‌توان نوشت:

و اما KS=JC-RC

بنابراین

LG=JC-IC

(۲۰)

MH=JC-EC

(۲۱)

از (۱۹)، (۲۰) و (۲۱) داریم:

(۲۲) = حجم باقی‌ماندۀ داخلی V-

از طرفی

=حجم باقی‌ماندۀ خارجی V+

پس:

(۲۳) = حجم باقی‌ماندۀ خارجی V+

در نتیجه باتوجه به اینکه فرمولهای (۲۲) و (۲۳) پس از تقسیم JB به ۲۲ قسمت مساوی به دست آمده، ملاحظه می‌کنیم که پس از تقسیم JB به ۲n قسمت مساوی (nєIN) داریم:

= حجم باقی‌ماندۀ داخلی V-

= حجم باقی‌ماندۀ خارجی V+

از (۱۴) و داریم:

< حجم باقی‌ماندۀ داخلی V-

و از (۱۵) و داریم:

> حجم باقی‌ماندۀ خارجی V+

با توجه به W=πJC۲.JB

و نیز و داریم:

(۲۴) < حجم باقی‌ماندۀ داخلی V-

(۲۵) > حجم باقی‌ماندۀ خارجلی V+

اکنون ابن‌هیثم فرض می‌کند که V

و دو حالت در نظر می‌گیرد:

حالت اول: V>

در این حالت فرض می‌کنیم s=V-

درنتیجه s عددی است مثبت. پس یک m وجود دارد، به‌طوری که s > ، پس برای n>m داریم: V- =S

< البته در منظور از حجم باقی‌ماندۀ داخلی متناظر با تقسیم JB به ۲n قسمت مساوی است. از داریم:

> حجم باقی‌ماندۀ داخلی V-

و این نامساوی متناقض با (۲۴) است. این تناقض نشان می‌دهد که حالت اول ممکن نیست.

حالت دوم: V<

مجدداً فرض می‌کنیم s= -V

و یک m موجود است، به‌طوری که s > برای هر n>m داریم:

-V=s

< البته در (۲۶) منظور حجم باقی‌ماندۀ خارجی متناظر با تقسیم JB به ۲n قسمت مساوی است. از (۲۶) داریم:

< حجم باقی‌ماندۀ خارجی V+

و این نامساوی متناقض با (۲۵) است. این تناقض نشان می‌دهد که حالت دوم نیز غیرممکن است. پس ابن‌هیثم نتیجه می‌گیرد که

V=

شکل ۷

البته با نمادهای امروزی توسط انتگرال‌گیری حجم حاصل از دوران قوس BC از سهمی ABC حول محور xها (شکل ۷) مساوی است با:

V=

و حجم حاصل از دوران مستطیل CB حول محور xها مساوی است با

W=πα۲r۵

بنابراین: V=

مسألۀ ۵

حجم حاصل از دوران قسمت هاشور خورده در شکل ۸ حول محور ZB مساوی است با حجم استوانۀ قائم مستدیری که ارتفاع آن QB و شعاع قاعدۀ آن فاصله نقطۀ T از خط ZB است (قابل ذکر است که در شکل ۸ نقاط T، Z، B، Q، d و خط L و سهمی ACB مانند شکل ۴ انتخاب شده‌اند).

در اینجا اثبات ابن‌هیثم را برای این مسأله بیان نمی‌کنیم، ولی مانند مسألۀ ۲ در مورد آن عمل می‌کنیم:

= مساحت هاشور خورده

مرکز ثقل قسمت هاشورخورده را با ( ، ) نمایش می‌دهیم، داریم:

درنتیجه فاصلۀ مرکز ثقل قسمت هاشور خورده در شکل ۸ از خط BZ (باتوجه به اینکه معادلۀ خط BZ عبارت است از (y=۲α d(r-x) مساوی است با

شکل ۸

درنتیجه مطابق قضیۀ پاپوس حجم حاصل از دوران قسمت هاشور خورده، حول محور BZ (یعنی V) عبارت است از فاصلۀ طی شده توسط مرکز ثقل ضرب در مساحت هاشورخورده، یعنی:

باتوجه به اینکه فاصلۀ T از خط BZ مساوی است با

و اینکه

پس حجم استوانۀ مورد بحث در صورت مسأله، مساوی است با

و بنابراین: V=

مسألۀ ۶

حجم حاصل از دوران قسمت هاشور خورده در شکل ۹ حول محور مساوی است با حجم استوانۀ قائم مستدیری که شعاع آن مساوی فاصلۀ نقطۀ T و ارتفاع آن مساوی است (در شکل ۹ نقطۀ T و خط L و سهمی ACB مانند شکل ۴ انتخاب شده اند، خطوط L و با هم موازی هستند و موازی محور سهمی است). مشابه مسألۀ ۵ می‌توان نشان داد که حجم استوانۀ مورد بحث مساوی با

و حجم حاصل از دوران قسمت هاشور خوردۀ شکل ۹ مساوی است.

شکل ۹

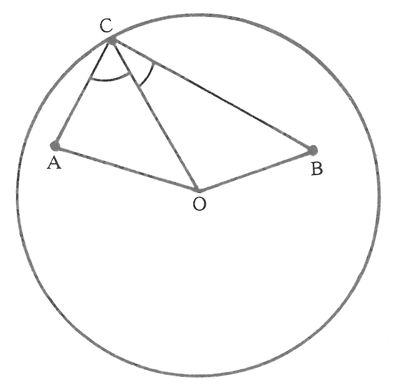
موضوع دیگری که در اینجا بررسی می‌شود، مسأله‌ای است به نام مسألۀ ابن‌هیثم که وی آن را در بخش ۵ کتاب المناظر اثبات کرده است. قابل توجه است که این مسأله حدود ۶۰۰ سال دانشمند را به خود مشغول کرده بود و نتوانسته بودند راه حل جدیدی برای آن به دست آورند و سرانجام در سدۀ ۱۷ م ریاضی‌دانان از جمله هویگنِس[۱] (۱۶۲۹-۱۶۹۵ م) روشهای جدیدی برای حل این مسأله یافتند.

مسأله چنین است: دو نقطه مانند A و B مفروض است (A نقطه‌ای نورانی و B چشم ناظر) و یک سطح آیینه‌ای مانند S داده شده است. مطلوب است تمام نقاط S به‌طوری که نور از نقطۀ A به S برخورد کرده و از نقطۀ B بگذرد.

این مسأله در مورد آیینه‌های کروی و استوانه‌ای به مسألۀ زیر منجر می‌شود:

دایره‌ای به مرکز O مفروض است. نقاط A و B داخل دایره (یا خارج آن) قرار دارند. مطلوب است تعیین همۀ نقاط مانند C روی دایره، به‌طوری که داشته باشیم:

AĈO = BĈO (۲۸)

شکل ۱۰

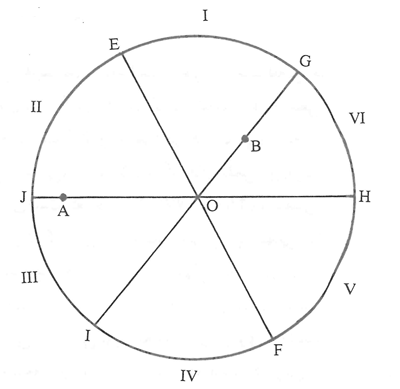
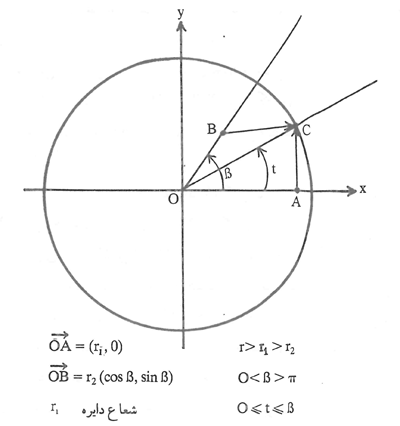
در شکل ۱۰، A و B را داخل دایره فرض کرده‌ایم و در اینجا می‌توان تصور نمود که A نقطه‌ای است نورانی، B چشم ناظر است و شعاعی که از A گذشته به سطح شفاف آیینه (که داخل کره یا استوانه فرض شده) برخورد کرده و به چشم ناظر در نقطۀ B رسیده، در نقۀ C به دایره (آیینه) برخورد کرده است. ابن‌هیثم ثابت کرده است که اگر نقاط B، O و A بر یک استقامت نباشند و OA≠OB (در شکل فرض شده OA>OB و در بحث پایین نیز همین فرض شده است. حالت OA=OB قبل از ابن‌هیثم توسط بطلمیوس حل شده بود)، در این صورت (هوخندایگ، ۱۰۸-۱۰۹؛ نیز نک‌ : شکل ۱۱) اگر نیمساز زاویۀ AÔB را رسم کنیم تا دایره را در نقاط E و F قطع کند، قطرهایی که از A و B می‌گذرند، همراه با قطر EF دایرۀ مزبور را به ۶ کمان مانند شکل ۱۱ تقسیم می‌کنند (کمانهای I تا VI). ابن‌هیثم ثابت کرده است که روی کمان II (بدون نقاط انتهایی E و J) دقیقاً یک نقطۀ C موجود است، به طوری که رابطه (۲۸) برقرار است. همچنین روی کمان V دقیقاً یک نقطۀ C(H وC≠F) موجود است، به‌طوری که رابطۀ (۲۸) برقرار است. روی کمانهای III و IV، نقطۀ ای که در (۲۸) صدق کند، وجود ندارد و سرانجام روی کمان VI (بدون نقاط انتهایی G و H) شمار Cهایی که در (۲۸) صدق می‌کنند ۱,۰ یا ۲ است و این شمار بستگی به مواضع A و B دارد. روش ابن‌هیثم برای اثبات این مسأله بسیار پیچیده، طولانی و دشوار است. به همین دلیل این روش را به رغم آنکه ــ به‌ویژه برای دوران ابن‌هیثم ــ یک کار بزرگ ریاضی به‌شمار می‌رود، در اینجا می‌آوریم، ولی مناسب است بدانیم که با روشهای امروزی وجود نقطه‌ای مانند C روی کمان II در شکل ۱۱ که در (۲۸) صدق کند، چگونه ثابت می‌شود. شرایط مسأله را در زیر شکل ۱۲ به صورت ریاضی نوشته‌ایم. شرط لازم و کافی برای اینکه نقطۀ C:r (Cos t, Sin t) در (۲۸) صدق کند. این است که خط OC نیمساز زاویۀ BCA باشد و این معادل است با اینکه تساوی (۲۹) در زیر برقرار باشد.

(۲۹)

(. در (۲۹) همان ضرب داخلی اقلیدسی است و ॥ همان نُرم معمولی اقلیدسی است) و این معادل است با اینکه

(۳۰)

ولی همیشه یک موجود است که در (۳۰) صدق کند، زیرا اگر طرف چپ (۳۰) را با φ(t) نمایش دهیم و طرف راست آن را با λ(t) نمایش دهیم، ملاحظه می‌کنیم که

شکل ۱۱

شکل ۱۲

پس تابه پیوستۀ λ-φ در نقطۀ صفر مثبت و در نقطۀ منفی است پس در نقطه‌ای بین صفر و مساوی صفر است. یعنی یک موجود است، به‌طوری که φ(t۰)-λ(t۰)=۰ یعنی φ(t۰)=λ(t۰) یعنی (۳۰) برای t=t۰ برقرار است، درنتیجه (۲۹) که با (۳۰) معادل است، برای C=r(Cost۰, Sin t۰) برقرار است. در نتیجه وجود نقطه‌ای مانند C روی کمان II در شکل ۱۱ که در (۲۸) صدق کند، ثابت می‌شود. توجه شود که برای رسیدن به یک اثبات سریع برای وجود C که در (۲۸) صدق کند، کافی است ملاحظه کنیم که

شکل ۱۳

واضح است که (۳۰) تمام جوابهای ممکن مسأله را برای ۰≤t≤β به دست می‌دهد. کتاب المناظر ابن‌هیثم که مسألۀ فوق در آن حل شده، بر مبنای کتابهای نور اقلیدس و بطلمیوس نوشته شده، ولی همان‌طور که به عنوان نمونه در مسألۀ بالا آمده، این کتاب شامل مطالب جدید و اثباتهای نوست. کتاب مزبور توسط یوهانس کپلر به کار گرفته شده است. ابن‌هیثم عقیدۀ بطلمیوس و اقلیدس را که اشعۀ نور از چشم به طرف شیء می‌رود، رد کرده و جهت آن را از شیء به طرف چشم می‌داند. ابن‌هیثم در این کتاب ثابت می‌کند که شعاع تابش و شعاع انعکاس و خط عمود بر سطح آیینه در نقطۀ برخورد شعاع به آیینه در یک صفحه واقعند و با عمود مزبور زوایای مساوی می‌سازند (نک‌ : شکل ۱۳ که AO شعاع تابش، OB شعاع انعکاس، O محل برخورد آنها با آیینه، OL عمود بر آیینه در نقطۀ O است. اولاً OB, OAو OL در یک صفحه واقعند، ثانیاً ). از تحقیقات و بررسیهای نسخه‌های خطی باقی‌مانده از ابن‌هیثم که تاکنون انجام شده، معلوم می‌شود که ابن‌هیثم در نجوم بیشتر به مسائل فرعی و حل آنها که البته از اهمیت برخوردار هستند (از جمله تعیین دقیق سمت قبله و ارتفاع ستارگان)، پرداخته است که همپایه با شاهکارهای او در ریاضیات و فیزیک (نور) نبوده است.

مآخذ

ابن ابی اصیبعه، احمد بن قاسم، عیون الانباء، به کوشش آوگوست مولر، قاهره، ۱۸۸۲ م / ۱۲۹۹ ق؛ ابن عبری، غریغوریوس بن هارون، تاریخ مختصر الدول، بیروت، ۱۹۵۸ م؛ ابن‌هیثم، حسن بن حسن، الشکوک علی بطلمیوس، به کوشش عبدالحمید صبره و نبیل شهابی، قاهره، ۱۹۷۱ م؛ بخیت، محمد عدنان، فهرس المخطوطات العربیة المصورة، اردن، ۱۴۰۶ ق / ۱۹۸۶ م؛ بیهقی، علی بن زید، تتمة صوان الحکمة، به کوشش محمد شفیع، لاهور، ۱۳۵۱ ق؛ اعلام؛ سارتن، جورج، مقدمه بر تاریخ علم، ترجمۀ غلام‌حسین صدری افشار، تهران، ۱۳۵۰ ش؛ شهرزوری، محمد بن محمود، نزهة الارواح، به کوشش سید خورید احمد، حیدرآباد دکن، ۱۳۹۶ ق / ۱۹۷۶ م؛ صاعد اندلسی، طبقات الامم، به کوشش لویس شیخو، بیروت، ۱۹۱۲ م؛ صبره، عبدالحمید، مقدمه بر الشکوک (نک‌ : هم‌ ، ابن‌هیثم)؛ قفطی، علی بن یوسف، تاریخ الحکماء، اختصار زوزنی، به کوشش یولیوس لیپرت، لایپزیک، ۱۹۰۳ م؛ نظیف بک، مصطفی، الحسن بن هیثم، قاهره، ۱۴۹۲ م؛ نیز:

Ahlwards, GAL; GAS; Hogendijk, J. P., Ibn al Haytham’s Completion of the Conics, Berlin, 1985; Khalidov; Loth, Otto, A Catalogue of the Arabic Manuscripts in the Library of the India Office, Leipzig, 1877; Sabra, A. I., «Ibn al Haytham», Dictionary of Scientific Biography, New York, 1972, vol. VI; Schoy, Carl, «Abbandlung des al-Ħasan ibn… al-Haitam… über die Bestimmung der Richtung der Qibla», ZDMG, Leipzig, 1921, vol. LXXV; Schramm, Mathias, Ibn al-Haythams Weg zur Physik, Wiesbaden, 1963; Widemann, E., Gesammelte Schriften zur arabisch islamischen Wissenschaftsgeschichte, Frankfurt, 1984; Voorhoeve.

علیرضا جعفری نائینی